Streaming Graph Neural Networks笔记

Streaming Graph Neural Networks笔记 该论文提出了DGNN模型

The update component

interact unit

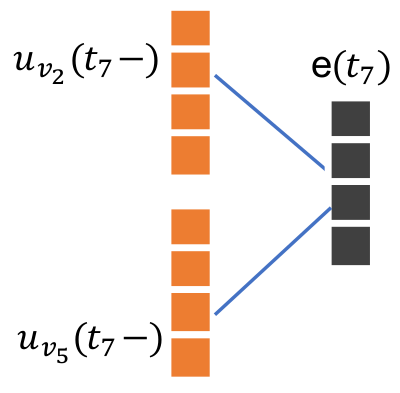
$$ e(t)=act(W_1 \cdot u_{v_s}(t-)+W_2 \cdot u_{v_g}(t-)+b_e)$$
其中$u_{v_s}$和$u_{v_g}$是点在时间t之前的特征，$W_1$和$W2$以及$b_e$是神经网络的参数,$act(\cdot)$是激活函数。$e(t)$包含了${v_s, v_g, t}$的交互的信息。

update unit

updata unit将经过intercact unit的节点信息更新。当许多interactions作用于同一节点时，update unit将遗忘以前的interactions。这操作和LSTM很像，所以论文魔改了LSTM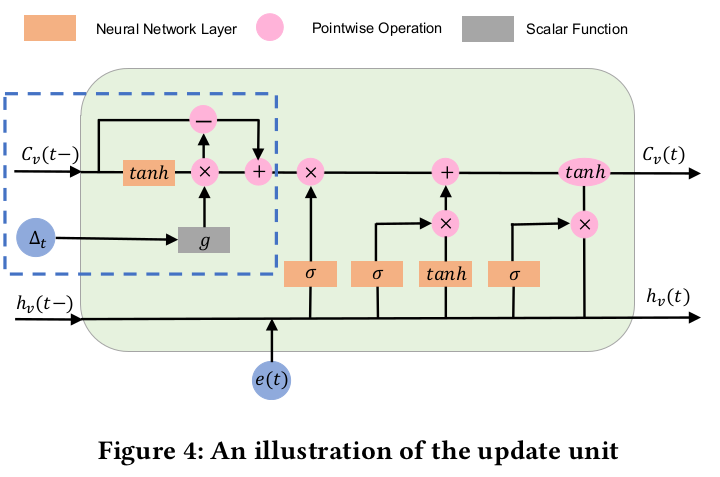

其中target node和source node是用的两个不同的update unit，结构相同，参数不同。update unit和LSTM不同的地方在蓝色虚线中，相当于改变了LSTM中$C$的输入。
公式：
$$C^I_v(t-1) = tanh(W_d \cdot C_v(t-1)+b_d)$$

$$\hat{C}^I_v(t-1)=C^I_v(t-1)*g(\Delta t)$$

$$C^T_v(t-1)=C_v(t-1)-C^I_v(t-1)$$

$$C^*_v(t-1)=C^T_v(t-1)+\hat{C}^I_v(t-1)$$
其中$C^I_v$由神经网络生成，代表短期记忆，短期记忆会随着时间遗忘，所以短期记忆会乘上$g(\Delta t)$ 得出$\hat{C}^I_v$，来表示遗忘后的短期记忆，$g(\Delta t)$是遗忘函数，$\Delta t$越长，其值越小。$C^T_v$是长期记忆，值不随时间而改变。$C^*_v(t-1)$是调整之后的$C$，作为标准LSTM的输入。后面就是LSTM的内容了。
$$ f_t=\delta(W_f \cdot e(t) + U_f \cdot h_v(t-1)+b_f) $$
$$i_t=\delta (W_i \cdot e(t) + U_i \cdot h_v(t-1)+b_i)$$
$$o_t = \delta (W_o \cdot e(t) + U_o \cdot h_v(t-1)+b_o)$$
$$\tilde{C}(t)=tanh(W_c \cdot e(t) +U_c \cdot h_v(t-1)+b_c)$$
$$C_v(t)=f_t * C^*_v(t-1)+i_t *\tilde{C}_v(t)$$
$$ h_v(t) = o_t * tanh(C_v(t))$$

值得注意的是，target和source node是用了两个不同的update unit。source update 只更新source node，同理target update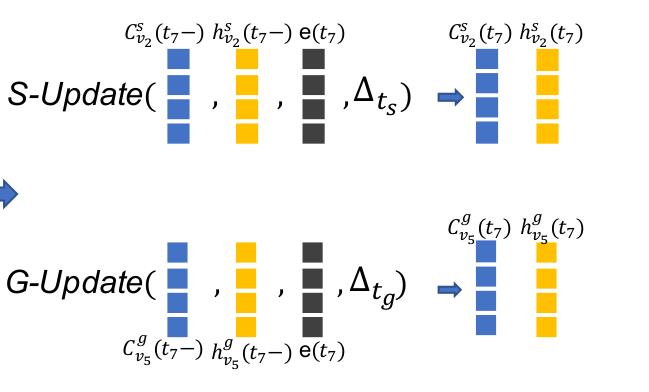

The merge unit

该unit是将当前生成的信息与之前的信息融合，形成$u_v(t)$
source node 公式：
$$u_{v_s}(t) = W^S \cdot h^S_{v_s}+W^g \cdot h^g_{v_s}(t-)+b_u$$
同理target node:
$$u_{v_g}(t)=W^S*h^S_{v_g}(t-)+W^g \cdot h^g_{v_g}(t) +b_u$$

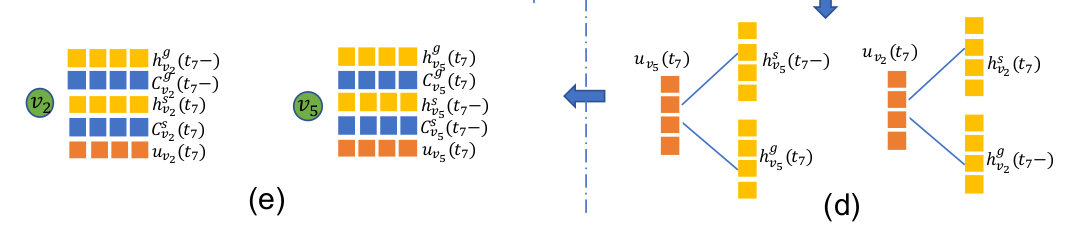
整个update component 的流程：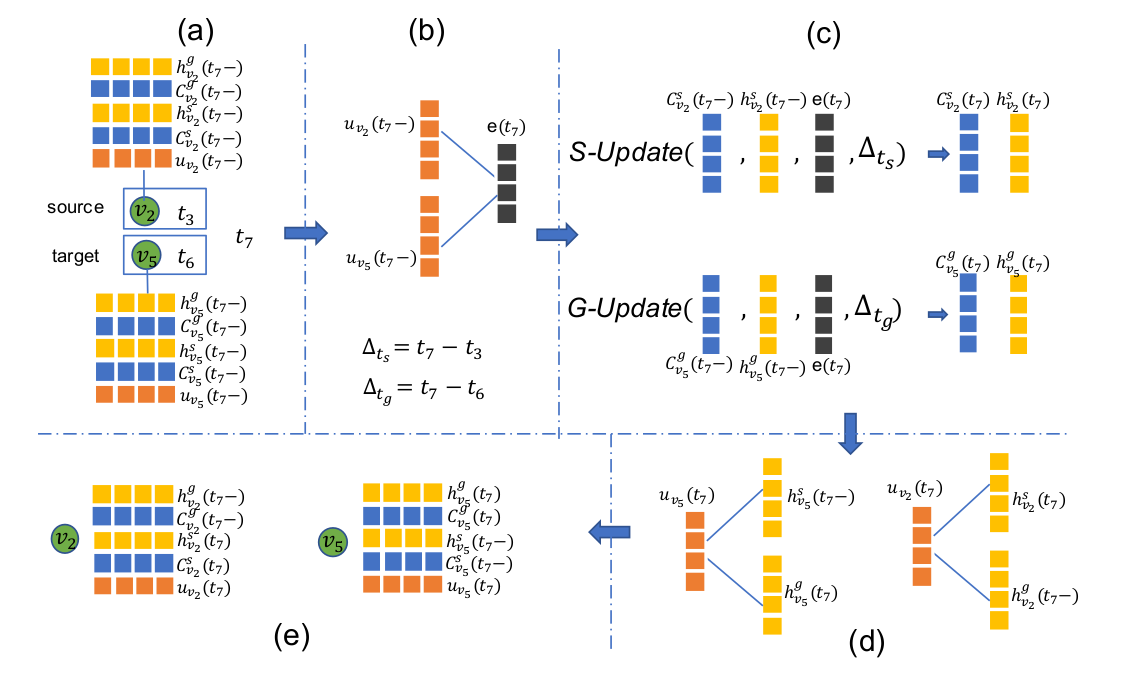

The propagation component

update component 只考虑连接建立起来时，两点的相互作用，而propagation component 则是将这两点的交互信息带入邻居节点中。影响邻居节点的方式不是像update component 那样修改cell memory的历史，而是给cell memory增添新的信息。

符号表示

$N^S(\cdot)$表示该点的source邻居的集合，$N^g(v_g)$表示该点target邻居的集合。
$$N(v_s)=N^s(v_s) \cup N^g(v_s)$$
$$N(v_g)=N^s(v_g) \cup N^g(v_g)$$

prop unit四种类型

• source node $v_s$到它的source邻居$N^s(v_s)$
• source ndoe $v_s$到它的target邻居$N^g(v_s)$
• target node $v_g$到它的source邻居$N^s(v_g)$
• target node $v_g$到它的target邻居$N^g(v_g)$

这四种类型的prop unit结构相同，参数不同。在论文中只提供了第一种的描述，其他类型类比即可。

propagate interaction information forrmulations

$$C^s_{v_x}(t)=C^s_{v_x}(t-)+f_a(u_{v_x}(t-), u_{v_s}(t-))\cdot g(\Delta ^s_t) \cdot h(\Delta ^s_t) \cdot \hat{W}^s_s \cdot e(t)$$
$$h^s_{v_x}(t)=tanh(C^s_{v_x}(t))$$
其中$v_x\in N^s(v_s)$，
而$\Delta^s_t=t-tx$代表了当前时间$t$与节点$v_x$与节点$v_s$发生交互的时间$t_x$的时间间隔。
$f_a$是和update component中定义$f_a$是同一个衰减函数。
$W^s_s$是传给source邻居交互信息的线性变换。

函数h的定义

$$h(\Delta ^s_t)=
\begin{cases}
1, \Delta^s_t\le \tau,\
0, otherwise.
\end{cases}$$
$\tau$是一个超参，如果时间间隔大于这个值，那么就代表时间间隔太大了。我们就不会向这个点传递交互信息。

$f_a$的定义

$f_a$是捕获$v_s$和$v_x$之间连接强度的注意力函数
$$f_a(u_{v_x}(t-),u_{v_s}(t-))=\dfrac{exp(u_{v_x}(t-)^Tu_{v_s}(t-))}{\sum_{v\in N^s(v_s)} exp(u_v(t-)^Tu_{v_s}(t-))}$$

propagation流程图

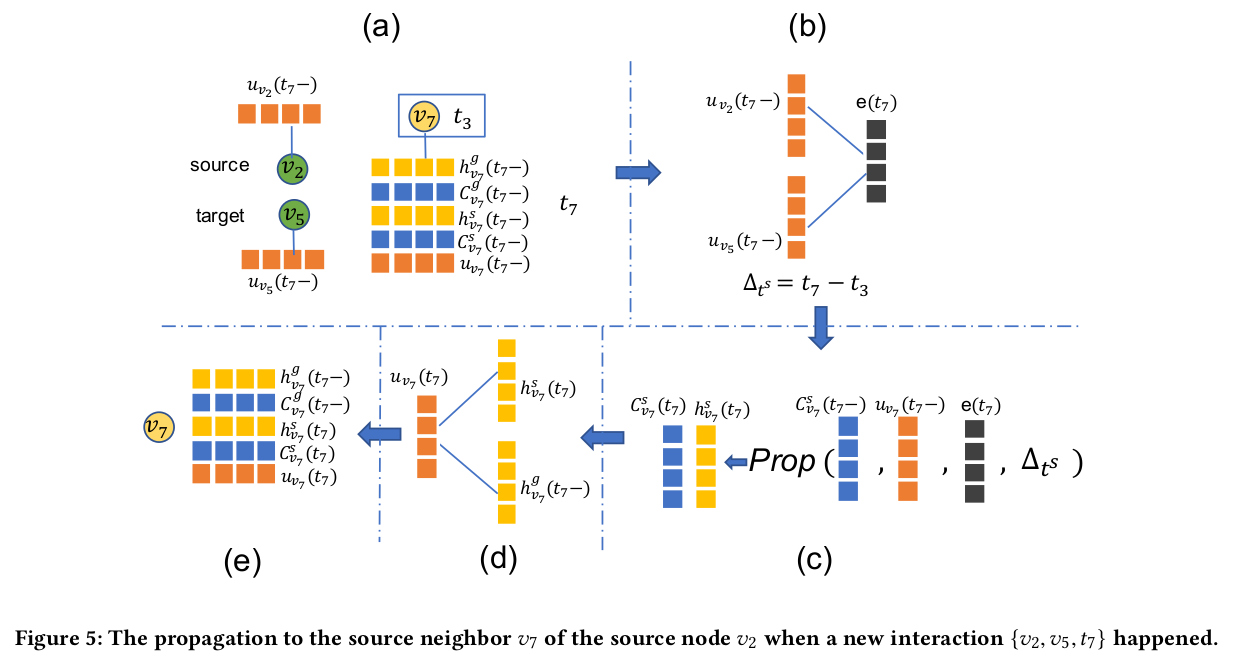
参数学习

Parameter learning for link prediction

link prediction 就是预测下一个连接关系。

projection matrix

projection matrix $P$是关于因变量(?英文名为response values)和预测值的映射。
$$\hat{y} = Py$$

$u^s_{v_s}(t-)$和$u^g_{v_g}(t-)$

论文中将$u_{v_s}(t-)$和$u_{v_g}$通过$P$投射到$u^s_{v_s}(t-)$和$u^g_{v_g}(t-)$

$$u^s_{v_s}(t-)=P^s \cdot u_{v_s}(t-)$$
$$u^g_{v_g}(t-)=P^g \cdot u_{v_g}(t-)$$

loss function

对于$v_s$和$v_g$出现的概率，用
$$\sigma (u^s_{v_s}(t-)^T u^g_{v_g}(t-)) $$
$\sigma(\cdot)$代表sigmod函数。
loss function:

$$ J((v_s, v_g, t))=-log(\sigma (u^s_{v_s}(t-)^T u^g_{v_g}(t-)))-Q \cdot \mathbb E_{v_n\sim P_n(v)}log(\sigma (u^s_{v_s}(t-)^T u^g_{v_g}(t-)))$$

$Q$是负采样的数量，$P_n{v}$是一个负采样的分布。

total loss:

$$ \sum_{e\in \mathcal{E}(T)}J(e) $$

其中$\mathcal{E}(T)$代表时间$T$之前的所有交互。

训练方法

采用mini-batch进行优化，并且mini-batch中边的样本是通过交互的时间序列采样的。mini-batch的loss通过所有在其中的交互计算的。负采样的分布$P_n(v)$是一个在mini-batch外所有点的标准分布，包括了交互的点和受影响的点。